The Good Bad Ugly of R-Square

MSE

• Sensitive to outliers
• Has the same units as the response variable.
• Lower values of MSE indicate better fit.
• Actually, it’s hard to realize if our model is good or not by looking at the absolute values of MSE or MSE.
• We would probably want to measure how much our model is better than the constant baseline.

Disadvantage of MSE

• If we make a single very bad prediction, taking the square will make the error even worse and
  • it may skew the metric towards overestimating the model’s badness.
• That is a particularly problematic behaviour if we have noisy data (data that for whatever reason is not entirely reliable) 
• On the other hand, if all the errors are smaller than 1, than it affects in the opposite direction: we may underestimate the model’s badness.

R-square

• proportional improvement in prediction of the regression model, compared to the mean model (model predicting all given samples as mean value).
• interpreted as the proportion of total variance that is explained by the model.
• relative measure of fit whereas MSE is an absolute measure of fit
• often easier to interpret since it doesn’t depend on the scale of the data.
  • It doesn’t matter if the output values are very large or very small,
• always has values between -∞ and 1.
• There are situations in which a high R2 is not necessary or relevant.
• When the interest is in the relationship between variables, not in prediction, the R2 is less important

Caution of R-square

For example: there is a linear regression: BMI ~ weight + height **(wrong model) ** R2 = 0.9 ln(BMI) ~ ln(weight) + ln(height) **(right model) ** R2 = 0.88

why?

1. It’s not out of sample evaluation! We should withhold part of data to evaluation a model

2. R square is methmetically flaw. $R^{2} = \frac{\sum (\hat{y} – \bar{\hat{y}})^{2}}{\sum (y – \bar{y})^{2}}$

   • R-squared does not measure goodness of fit. It can be arbitrarily low when the model is completely correct. By making σ2 large, we drive R-squared towards 0, even when every assumption of the simple linear regression model is correct in every particular.
   • What is σ2 ? When we perform linear regression, we assume our model almost predicts our dependent variable. The difference between “almost” and “exact” is assumed to be a draw from a Normal distribution with mean 0 and some variance we call σ2 .
   • R-squared can be arbitrarily close to 1 when the model is totally wrong. Let’s recap:

• R-squared does not measure goodness of fit.
• R-squared does not measure predictive error.
• R-squared does not allow you to compare models using transformed responses.
• R-squared does not measure how one variable explains another.

MSE vs R-square

1. $MSE$ measures how far the data are from the model’s predicted values

2. $R^2$ measures how far the data are from the model’s predicted values compare to how far the data are from the mean

The difference between how far the data are from the model’s predicted values and how far the data are from the mean is the improvement in prediction from the regression model.

RMSE and RMSLE

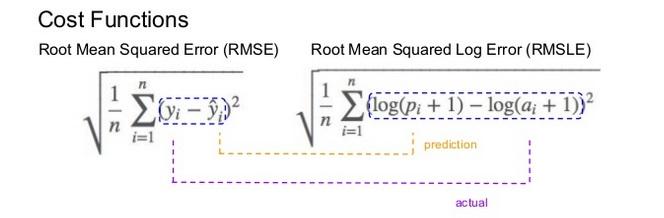
Mechanism

• It is the Root Mean Squared Error of the log-transformed predicted and log-transformed actual values.

• RMSLE adds 1 to both actual and predicted values before taking the natural logarithm to avoid taking the natural log of possible 0 (zero) values.

• As a result, the function can be used if actual or predicted have zero-valued elements. But this function is not appropriate if either is negative valued

• RMSLE measures the ratio of predicted and actual.

  $log(p_i +1) − log(a_i+1)$

  can be written as 𝑙𝑜𝑔((𝑝𝑖+1)/(𝑎𝑖+1))

RMSLE is preferable when

• targets having exponential growth, such as population counts, average sales of a commodity over a span of years etc

• we care about percentage errors rather than the absolute value of errors.

• there is a wide range in the target variables

• we don’t want to penalize big differences when both the predicted and the actual are big numbers.

• we want to penalize under estimates more than over estimates.

  Lets have a look at the below example

  Case a) : Pi = 600, Ai = 1000 (under estimate)

  RMSE = 400, RMSLE = 0.5108

  Case b) : Pi = 1400, Ai = 1000 (over estimate)

  RMSE = 400, RMSLE = 0.3365

  As it is evident, the differences are same between actual and predicted in both the cases. RMSE treated them equally however RMSLE penalized the under estimate more than over estimate.

MSE incorporates both the variance and the bias of the predictor. RMSE is the square root of MSE. In case of unbiased estimator, RMSE is just the square root of variance, which is actually Standard Deviation.

In case of RMSLE, you take the log of the predictions and actual values. So basically, what changes is the variance that you are measuring.

• If both predicted and actual values are small: RMSE and RMSLE is same.
• If either predicted or the actual value is big: RMSE > RMSLE
• If both predicted and actual values are big: RMSE > RMSLE (RMSLE becomes almost negligible)

Sources: